Aimfract/Images fractales
    [home] Home         [no previous]         [no previous]         [no previous]    

Images fractales d'Aimfract

Menu Image

Les images que vous allez voir et dessiner sont des fractales.
A chaque image est associ un nom et des paramtres qui servent pour les algorithmes de calcul.
Et voici quelques ides en cas de problmes.


Charger

Vous la choisissez dans la fentre de chargement.
L'image qui sera charge sera aussitt affiche et ses paramtres seront mis dans les tableaux des paramtres.


Lancer

S'affiche une page blanche o va apparatre peu peu une image au fur et mesure de son calcul d'aprs ses paramtres.
En appuyant sur une touche, cela s'arrte (sauf pendant le contournage) et vous pouvez la sauver pour la terminer plus tard.
Les lignes calcules sont choisies au hasard ce qui permet d'avoir assez vite une bonne ide de l'image.


Terminer

On finit le calcul et le dessin de l'image l'cran. Cela sert galement charger l'image de l'cran vers la mmoire pour sauver ce qui se trouve l'cran.


Repre

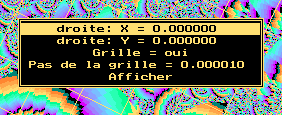Menu du reprage
  • Valeur de X
  • Valeur de Y
  • Grille
  • Pas de la grille
  • Afficher

Vous pouvez afficher des droites permettant de vous reprer sur le dessin, par exemple, pour voir o est le point (0,0), vous choisissez dans le menu qui va s'afficher 0 pour X et 0 pour Y, en cliquant sur Afficher vous voyez apparatre 2 droites, leur point de croisement est (0,0).

La droite x = la valeur choisie sera affiche (couleur 12) si votre nombre X est suprieur Gauche et est infrieur Gauche+Largeur.
La droite y = la valeur choisie sera affiche (couleur 12) si votre nombre Y est suprieur Bas et est infrieur Bas+Hauteur.

Grille sur mandel Si Grille est oui, alors des droites s'afficheront (couleur 5) ayant le Pas de la grille en cart aussi bien vertical qu'horizontal.

Par dfaut, les droites ne sont pas sauvegards avec l'image. Si vous les voulez, aprs les avoir affiches, vous faite Terminer puis vous sauvez l'image.


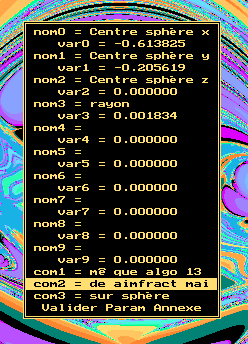Paramtres annexes

Paramtres annexes Ils servent si votre algorithme est dans un fichier de formules.

Vous pouvez donner un nom pour chaque variable utilise (10 en tout) et commenter votre image grce aux trois avant-dernires lignes. Chaque nom a une longueur de 19 caractres maximum et chaque commentaire de 29 caractres.

La dernire ligne sert valider.


Info lettre

Paramtres pour les lettres

Vous pouvez crire un texte sur votre dessin, chaque lettre est constitue de rectangles et d'arcs de cercle (elles sont dcrites dans le fichier LETTRES.DES). Chaque composant est vu comme un volume (cylindre ou portion de sphre) refltant l'image et c'est ce reflet qui donnera la lettre.

On ne peut crire qu'une ligne sur une image ; pour en avoir plusieurs, il faudra plusieurs morceaux d'image qui, se superposant, composeront le texte voulu.
Ex : voir le scnario LETTRE.SNR.


Ajot Lettre

Mis oui, il permettra d'crire sur l'image.


Multiplie l'paisseur

Ce paramtre multiplie l'paisseur des traits et des arcs de cercle formant les lettres. On considre sa valeur absolue.


Largeur

C'est le pourcentage de la largeur de l'cran que prendra votre texte. Du nombre de lettres et de la largeur choisie dpendra la hauteur, tant donn qu'une lettre s'inscrit dans un carr.
Ex : la largeur est de 100, il y a quatre lettres, donc la hauteur de la phrase est le quart de celle de l'image (si les dimensions de l'image respecte bien le rapport 3/4).


Position en Y

Ce paramtre sert positionner le milieu du texte en hauteur.
Ex : s'il est 50 votre phrase sera au milieu de l'cran pour la hauteur. 0 correspond au bas de l'cran et l'on verra la moiti haute.


Centr

Ce paramtre sert positionner votre texte dans la largeur.
Valeurs : 0 pour centrer, 1 pour positionner gauche, 2 pour positionner droite.


Sauve une partie

S'il est mis oui, alors ne sera calcule et sauve que le rectangle de l'image encadrant votre texte. Cela permet un gain de temps intressant et surtout la possibilit de recouvrir en partie une autre image.

Ex : Pour composer l'image avec le texte suivant :
       BONJOUR
       A TOUS
il faut, aprs avoir calcul les deux images ncessaires, charger l'image BONJ1 (qui est entire), la recouvrir avec l'image BONJ2 (qui est un morceau), mettre ce paramtre non, faire Terminer et finalement sauver. Et l'on obtient BONJOUR.


Eloignement

Plus il est grand, plus les volumes composant les lettres considres sont loin de l'image et en reflte une plus grande partie. S'il est 0, alors les volumes sont tangents l'image.


Grossissement

Il multiplie la taille des lettres et leur paisseur sans les carter les unes des autres. En ngatif, il inverse les lettres (le haut devient le bas et la droite devient la gauche).


Texte

Il se compose de un ou plusieurs mots qui seront crit sur une mme ligne. Le maximum est de 29 caractres.
Les lettres sont dcrites dans LETTRES.DES, seules les majuscules sont fournies plus - et a.
Vous pouvez complter ce fichier (voir lettre.doc).


Validation

Confirme la saisie des paramtres.



Paramtres

Les paramtres d'une image sont les lments ncessaires l'ordinateur pour le calcul de l'image.
Tous les paramtres qui sont des nombres virgule plus le paramtre de profondeur de calcul font changer continment l'image, c'est dire que si vous faite varier un peu le paramtre alors l'image changera un peu.

Liste des Paramtres

On considre que l'cran est une portion du plan complexe, chaque point sera vu avec une coordonne en x (l'axe horizontal) et une en y (l'axe vertical).

Quand vous choisissez un nouveau rectangle avec Gauche, Bas, Largeur, Hauteur et Angle, vous dlimitez un rectangle, de plus vous pouvez le dformer (allong en hauteur ou en largeur) en n'ayant pas Hauteur/Largeur=3/4.
Vous pouvez aussi le choisir avec la Souris.


Fichier de Formules

Grce ce fichier, vous allez pouvoir crire vos formules et voir les dessins rsultants. Par dfaut (pas de nom), vous avez 20 formules (codes de 0 19) dans le logiciel.

Comment l'crire : Dans un diteur de texte, vous crivez votre formule avec un numro d'algorithme, vous la sauvez au format ASCII avec l'extension frl.
Ensuite vous faites appel un utilitaire FORMULE.EXE qui rend votre formule assimilable par AIMFRACT.
Dans AIMFRACT, vous crivez votre nom de fichier Fichier de Formule, le bon numro Algorithme, ventuellement vous changez d'autres paramtres et alors le logiciel dessine votre image.
La mthode d'criture, ainsi que les conseils, sont expliqus dans FORMULE.DOC.

Dans votre Fichier de Formules, vous pouvez crire plusieurs formules, chacune devant avoir un numro d'algorithme diffrent.
Vous pouvez avoir plusieurs Fichiers de Formules.

Image d'une formule avec des paramtres annexes Les Paramtres Annexes vous fournissent de nouvelles variables.

FORMULE.EXE crit partir de votre fichier votre.frl un nouveau fichier votre.cop ou votre.emu, il essaye d'optimiser les calculs faire et crit les fonctions en langage machine afin d'optimiser les temps de calcul lors du dessin. Selon que vous avez Coprocesseur oui ou non, sera considr le fichier votre.cop ou votre.emu.


Algorithmes

Il y a 20 algorithmes numrots de 0 19, l'algorithme sert dterminer quel type de calcul est effectu par l'ordinateur.

Ce qui suit n'est pas ncessaire l'utilisation du programme.

Tous les algorithmes sont faits partir d'une fonction que l'on calcule de faon itrative, c'est dire f(0), f(f(0)), f(f(f(0))) ...
On arrte le calcul ds que la norme de f(z) est suprieure la Norme choisie ou que l'on a itr le calcul n fois (n tant la Profondeur choisie).
Le nombre de fois (k) que le calcul a t effectu sert dterminer la couleur.
La couleur 16 reprsente la convergence et les autres couleurs reprsentent quelle tape le calcul s'est arrt.
Par exemple, s'il a diverg au 31ime coup et que la Profondeur est de 150, il aura la 4ime couleur.
Le paramtre Tornade change la rpartition des couleurs.

Convergence : Lors du calcul d'un point, on recommence le calcul si la norme du rsultat est infrieure la Norme choisie, et ceci jusqu' ce que le nombre de calculs faits soit gal la Profondeur.
On dit qu'un point converge pour AIMFRACT si le nombre de calculs faits est gal la profondeur. Sa couleur est la 16ime.

Les fonctions utilises sont, entre autres,
norme(z) = racine(x+y) o z est un nombre complexe : z=x+iy
pow(z1,z2) indique z1 la puissance z2, z1 et z2 pouvant tre des complexes.

Si vous connaissez le langage C, voici le code de l'algo 0 :

  norm2 = norme*norme;
  if (puisr == 2)
  {
   for ( x = consx+(coord?x0:0), y = consy+(coord?y0:0), k = 0;
         k < profondeur && ((sx=x*x)+(sy=y*y)) < norm2; 
         k++)
   {
    y = 2*x*y+y0;
    x = sx-sy+x0;
   }
  }
  else
  {
   double r,teta;
   for ( x = consx+(coord?x0:0), y = consy+(coord?y0:0), k = 0;
         k < profondeur && (r=hypot(x,y)) < norme; 
         k++)
   {
    if (r != 0)
    {
     teta = acos(x/r)*puisr;
     if (y < 0) teta = -teta;
     r = pow(r,puisr);
     x = r*cos(teta);
     y = r*sin(teta);
    }
    y = y0+y;
    x = x0+x;
   }
  }

Mandel Algorithme 0 : Ensemble de Mandelbrot

C'est l'ensemble fractal le plus classique.
Pour cet ensemble la fonction que l'on itre est f(z)=z+p o p est le point du plan auquel on s'intresse (z et p sont des complexes).
On calcule ainsi

    f(p) = 0
    f(f(p)) = f(p)+p et ainsi de suite tant que norme(f(p)) < Norme

Ici le calcul a t agrment de paramtres supplmentaires de manire pouvoir obtenir des images drives de l'ensemble de Mandelbrot.
Ainsi tous les paramtres sauf Puissance imaginaire auront de l'effet. Dans le cas d'un ordinateur avec coprocesseur cet algorithme a t particulirement optimis.
Si l'on veut utiliser le mme algorithme que le 0 mais o Puissance imaginaire est utilis il faut utiliser le 18. Le 18 est bien plus lent (avec ou sans coprocesseur).

Algorithme 1

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + (z.x)-(z.y) - 2*i*z.x*z.y
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 2

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + z + 2*z.x*z.y + p.y
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 3

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = z + p.x*(2*z.x*z.y+p.y*z.x) + z.x+p.y
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 4

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + pow(z,PuisR+norme(p))
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 5

U(0)   = p +PuisI*(ConstX-p.x) + i*PuisI*(ConstY-p.y)
ConstX = ConstX + PuisI*(p.x-ConstX),
ConstY = ConstY + PuisI*(p.y-ConstY),
f(z)   = pow(z,PuisR) + ConstX + i*ConstY
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Le paramtre Puissance Imaginaire ne sert pas ici en tant que puissance mais est utilis pour passer de l'ensemble de Julia celui de Mandelbrot.
Si ce paramtre est gal 0, on a l'ensemble de Julia, s'il est gal 0.5, on trouve celui de Mandelbrot.

Algorithme 6

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + pow(z,norme(z)+2)
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 7

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + r*(ConstX*cos(theta*PuisR) + i*ConstY*sin(theta*PuisR))
o r = norme(z) et theta = l'angle de z modulo PI
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 8

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + pow(r,ConstX)*cos(theta*PuisR) + i*pow(r,ConstY)*sin(theta*PuisR)
o r = norme(z) et theta = angle de z modulo PI
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 9

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + i*2*z.x*z.y + (z.x) - (2*z.x*z.y+p.y)
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 10

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + (z.x)-(z.y) + i*2*z.y*((z.x)-(z.y)+p.x)
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 11

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + z.x*z.y + (z.y) + i*((z.x)-z.x*z.y)
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 12

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + z.x*z.y + z.x + i*(z.x*z.y+z.y)
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 13

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + z.y - z.x + i*(z.x*z.y-z.y)
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 14

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + ((z.x+z.y)+1)/((z.x)+1) + i*((z.x+z.y)+1)/((z.y)+1)
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 15

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + (z.x+z.y)/(z.x-z.y+1) + i*(z.x+z.y)/(z.x*z.y+1)
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 16

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = z.y-z.x + i*(z.x*z.y-z.y)
U(n+1) = f(U(n)) + p/(n+1)
Arrt quand norme(U(n)) >= Norme

Julia Algorithme 17 : Ensemble de Julia

U(0)   = p
f(z)   = pow(z,PuisR) + ConstX + i*ConstY
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Pour obtenir une belle image, il est intressant de prendre comme constante un des points qui se trouvent sur le bord de l'ensemble de Mandelbrot.

Algorithme 18 : Ensemble de Mandelbrot avec Puissance Imaginaire

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + pow(z,PuisR + i*PuisI)
U(n+1) = f(U(n))
Arrt quand norme(U(n)) >= Norme

Algorithme 19

U(0)   = p*Coord + ConstX + i*ConstY
f(z)   = p + exp(g(z) * (PuisR + i*PuisI))
avec si real(z) !=0, g(z) = log(norm(z))/2 + i*atan(imag(z)/real(z))
     sinon        , g(z) = log(abso(imag(z))) + i*(imag(z)<0 ? -PI/2 :PI/2)
U(n+1) = f(U(n))
Arrt quand racine(norme(U(n))) >= Norme

Profondeur

Algorithmes qui l'utilisent : tous
Valeurs possibles : entiers de 1 65500 (pas de ngatif)
Exemple de valeur : 50

C'est ce qui permet d'avoir un dessin plus (vers 65500) ou moins (vers 1) prcis.
Plus la profondeur est grande plus l'ordinateur s'applique (plus il calcule) mais s'appliquer ne sert rien sur des images assez simples, il se peut que les profondeurs 100 et 300 donnent pratiquement le mme dessin.


Puissance Relle (PuisR)

Algorithmes qui l'utilisent : 0,4,5,7,8,17,18,19
Valeurs possibles : tout rel
Exemple de valeur : 2

Certains algorithmes utilisent des puissances complexes (a + ib), a est la partie relle, c'est celle utilise pour les algorithmes n'utilisant que les puissances relles.


Puissance Imaginaire (PuisI)

Algorithmes qui l'utilisent : 5,18,19
Valeurs possibles : tout rel
Exemple de valeur : 0


Coordonnes (Coord)

Algorithmes qui l'utilisent : tous sauf les algorithmes 5 et 17
Exemple de valeur : non

Mettre Coordonnes oui revient ajouter p f(p) au premier coup (c'est dire f(p) = p et non f(p) = 0), ce paramtre n'a aucun effet les coups suivants.


Inversion

Algorithmes qui l'utilisent : tous
Exemple de valeur : non

Au lieu de prendre p comme point de dpart, on prend 1/p.
C'est plus lent car la procdure de contournage ne peut plus tre utilise ou rarement.
Comme exemple comparer les images : Mandel et Oeil


Contourne

Algorithmes qui l'utilisent : tous
Exemple de valeur : oui

Que fait contourne : Quand contourne est oui, lors du calcul de l'image, si le programme tombe sur un point de convergence, il va faire le tour de l'ensemble des points convergents qui touchent le point qu'il a trouv. Une fois le tour fait, il remplit l'intrieur de la couleur de convergence (16).

Inconvnient de contourne : Si dans l'image que l'on calcule, il y a une plage de non convergence qui est incluse dans une plage de convergence alors la plage de non convergence n'apparatra pas et sera remplace par la plage de convergence.
Ceci ne se produit pas pour l'ensemble de Mandelbrot, pour les autres dessins, si l'on n'est pas sr, on peut commencer par faire un petit test en commenant le calcul sans le contournage (en particulier si Inversion est oui ou si la Puissance Relle est ngative).

Avantage de contourne : Pour les plages de convergence, on ne calcule que les bords, or les points convergents sont les plus longs calculer. Avec contourne, quand on augmente la profondeur de calcul le temps de calcul total augmente faiblement.
Ceci est temprer par le fait que le bord de l'ensemble de Mandelbrot est de dimension 2 ! (et certainement pour pas mal d'autres images), il en rsulte que plus on va voir des dtails petits et tarabiscots de l'image, plus le bord de l'ensemble de convergence se comporte comme une surface et est donc long calculer.


Tornade

Algorithmes qui l'utilisent : tous
Exemple de valeur : non

Avec cette option oui, les couleurs sont rparties ainsi :
Les points qui convergent auront toujours la 16ime couleur,
les points qui divergent au (Profondeur-1)nime coup auront la 15ime couleur,
ceux qui divergent au (Profondeur-2)nime coup auront la 14ime couleur,...
ceux qui divergent au (Profondeur-15)nime coup auront la premire couleur,
ceux qui divergent au (Profondeur-16)nime coup auront la 15ime couleur, etc

Cela donne un effet de profondeur et peut aider reprer les plages de points divergeant en mme temps, l'idal serait d'avoir autant de couleurs que d'tapes de calcul possibles.


Constante X (ConstX)

Algorithmes qui l'utilisent : tous
Valeurs possibles : tout rel
Exemple de valeur : 0

X veut dire que l'on ajoute cette constante la partie relle.


Constante Y (ConstY)

Algorithmes qui l'utilisent : tous
Valeurs possibles : tout rel
Exemple de valeur : 0

Y veut dire que l'on ajoute cette constante la partie imaginaire.


Norme

Algorithmes qui l'utilisent : tous
Valeurs possibles : tout rel positif
Exemple de valeur : 2

C'est le point d'arrt du calcul : quand la norme du point calcul un moment de l'itration devient plus grande que celle que vous avez choisie ici, le calcul est fini et la couleur est dcide.
Si, tout moment de l'itration, la norme du point calcule est infrieure celle donne ici, le calcul s'arrte quand la Profondeur est atteinte et la couleur de ce point est celle de la convergence.
Dans les versions prcdentes (< 3), la norme tait dpendante de l'algorithme
ex : algo 10, norme = 3.


choix d'un carr avec la Souris

Cela permet de choisir un dtail de l'image. Avec la souris on choisit deux points du rectangle voulu.

Un menu s'affiche : Choix du bord pour la souris

  1. Il faut d'abord appuyer sur la touche b ou g :
    * b pour que les deux points que vous choisirez soient ceux du bas du rectangle. Le premier point choisi sera situ en bas gauche de la nouvelle image.
    * g pour que les deux points que vous choisirez soient ceux du ct gauche du rectangle. Le premier point choisi sera situ en haut gauche de la nouvelle image.
  2. Puis on clique sur deux points
  3. apparait alors le rectangle correspondant
  4. Si on n'est pas satisfait du rectangle, on recommence l'tape 2)
  5. Si on est content, on appuie sur Entre.
  6. Si on en a marre de ce truc, on fait Esc.
  7. Le tableau des Paramtres se raffichera alors avec dans le cas 5) les nouvelles valeurs pour Gauche, Largeur, Bas, Hauteur et Angle.

Gauche

Il dtermine quel point le ct gauche du cadre est proche ou non de l'axe vertical.
Ex : Mandel est moins 2 du point (0,0) avec une largeur d'environ 2.5, si vous choisissez Gauche -100, une largeur de 200, Bas -50 et une hauteur de 100, vous aurez un tout petit Mandel dform.


Bas

Il dtermine quel point le bas du cadre est proche ou non de l'axe horizontal.


Largeur

C'est la largeur totale en rel de votre image.


Hauteur

C'est la hauteur totale en rel de votre image.


Angle

C'est l'angle en degr de l'image par rapport l'horizontale.


Validation

Quand on a modifi les paramtres et que l'on veut garder les modifications, on choisit Valider, sinon on fait Esc.


Problmes

Les problmes recenss ici sont ceux pour lesquels il n'y a pas de messages d'erreur, pas de plantage, juste une image toute petite ou toute noire, pas de texte qui s'affiche ...

Vous n'arrivez pas sauver une image avec la grille affiche ou plusieurs lignes de texte ?

Vos lettres sont obliques, dformes en largeur ou en hauteur ... : la cause en est que l'image, sur laquelle elles sont crites, est dforme (il n'y a pas la proportion de 3/4 entre la Hauteur et la Largeur).


    [home] Home         [no previous]         [no previous]         [no previous]    
http://maretmanu.bobu.eu/homepage/aimfract/image.html
Date de cration : 7 juin 1997    Dernire modification : 14 December 2000